Problem 29: Distinct powers

*Difficulty: Easy

Problem:

Consider all integer combinations of a^b for 2 ≤ a ≤ 5 and 2 ≤ b ≤ 5:

2²=4, 2³=8, 2⁴=16, 2⁵=32
3²=9, 3³=27, 3⁴=81, 3⁵=243
4²=16, 4³=64, 4⁴=256, 4⁵=1024
5²=25, 5³=125, 5⁴=625, 5⁵=3125

If they are then placed in numerical order, with any repeats removed, we get the following sequence of 15 distinct terms:

4, 8, 9, 16, 25, 27, 32, 64, 81, 125, 243, 256, 625, 1024, 3125

How many distinct terms are in the sequence generated by a^b for 2 ≤ a ≤ 100 and 2 ≤ b ≤ 100?

How to solve:

Use Java (or any other programming languages that support big numbers)

Solution took 62 ms

I think that by mathematic analyze, we can point out how many duplicates numbers. For example, 100*100 is 10000, it means the maximum number of terms is 10000, but in 10000, there are possibly many numbers that are duplicated. Subtract 10000 from that, we got the answer. That will be way more faster than this, this is just merely brute force.

Problem 28: Number spiral diagonals

*Difficulty: Medium

Problem:

Starting with the number 1 and moving to the right in a clockwise direction a 5 by 5 spiral is formed as follows:

21 22 23 24  25
20  7    8   9  10
19  6    1   2  11
18  5    4   3  12
17 16 15 14  13

It can be verified that the sum of the numbers on the diagonals is 101.

What is the sum of the numbers on the diagonals in a 1001 by 1001 spiral formed in the same way?

How to solve:

I sat down and started analyzing the problem, after many tries, I figured out this solution:

We got 4 diagonals in total, 1 goes from 1 to 9, named sum1, 1 goes from 1 to 3, named sum2, 1 goes from 1 to 5, named sum 3, and one goes from 1 to 7, named sum 4 (4 different directions).

• The first four numbers on sum1 are 1,9,25,49

9-1 = 8 (base)

25-9 = 8*1 + base

49-25 = 8*2 + base

let i goes from 1 to n/2-1 (exclusive), n>=7, n is an odd number, cur1 is initialized with 9, base1 = 9-1 = 8, then sum1 will be calculated as

 

 

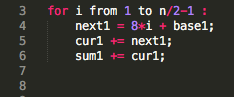
• The first four numbers on sum2 are 1,3,13,31

3-1 = 2 (base)

13-3 = 8*1 + base

31-3 = 8*2 + base

let i goes from 1 to n/2-1 (exclusive), n>= 7, n is an odd number, cur2 is initialized with 3, base2 = 3-1=2, then sum2 will be calculated as

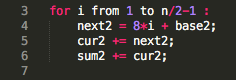
• The first four numbers on sum3 are 1,5,17,37

5 – 1 = 4 (base)

17-5 = 8*1 + base

37-17 = 8*2 + base

let i goes from 1 to n/2-1 (exclusive), n >= 7, n is an odd number, cur3 is initialized with 5, base3 = 5-1=4, then sum3 will be calculated as

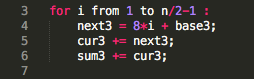
• Last but not least, the first four numbers on sum4 are 1,7,21,43

7-1 = 6 (base)

21-7 = 8*1+base

43-21 = 8*2+base

let i goes from 1 to n/2-1 (exclusive), n>=7, n is an odd number, cur4 is initialized with 7, base4 = 7-1=6, then sum4 will be calculated as

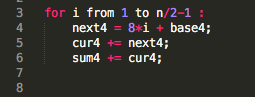
This is how you combine the 4 for-loop above:

There you go, if you reach here, means you’ve calculated the sum of all number (except 1) on all four diagonals. The last work you need to do is just adding sum1,sum2,sum3,sum4 and plus 1.

This way, you can calculate sum of all numbers on the diagonals in a spiral with any size >= 7. How about 1,3,5, sadly, you have to do it by yourself.

Solution took 0 ms with size = 1001